rhoadley.net music research software blogs
introduction through the sharp hawthorn in principio four archetypes sextet only connect shilbottle cobbles miscellaneous pieces scena concertino three pieces for two pianos conclusions bibliography
2
String Sextet
Originally: Still Life
Composed: Durham, June 1987
Revised: May 1988
Performed: Never. (Almost accepted for Huddersfield CMF (too long); accepted for performance in University of York Music Project, but withdrawn.)
Tape: Recording of MIDI sequence file included
The String Sextet was originally written as an entry for the Huddersfield Contemporary Music Festival's 1987 Composition Competition. It was submitted under the title Still Life.
2.1 Compositional Methods
2.1.1 Contour
One of the most interesting influences on the composition of the Sextet was the work I was then doing on Durham's PDP-11 computer. Although usually used to generate sound using the Music 11 programme, I had branched out slightly and was exploring the use of the computer to generate melodic lines from arrays of random numbers. I had become interested in this, not out of any desire to imitate any particular style, (a very complex project primarily involving analytical studies), but from an interest in the use of contour rather than specific melodic sequences as material. This in turn related to an unhappiness on my part with the standard methods of twelve-tone composition, and yet a personal affinity with the use of contrapuntal textures. I was constantly finding the need for sequences of varied yet related melodic streams, primarily for textural purposes. In these circumstances the act of composition itself often 'coloured' the sound of these streams, if only because of the quantity of notes involved and the presence of musical 'ticks' that kept recurring in an unwelcome manner, and yet the desire to escape from the sound of this.
Anyway, the use of 'randomly generated' melodic streams seemed a good solution at the time. As I had no experience of computer programming, I had to go through a number of stages in order to achieve the effect I desired, and one of the interesting parts of the work was finding out just how complex musical 'forms' actually are, and how many things are taken for granted by musicians when composing even the most simple sequences. Obviously, a sequence of random numbers by itself proved very little use. It is one of the features of randomness that although on a 'global' scale, results are predictable and uniform, but on a 'local' level, quite distinctive features appear. These are usually undesirable. The use of the melodic streams was to achieve unpredictable and yet stylistically desirable results.
The first and most obvious stage was to produce 'melodies' of a similar contour. Some of the most basic gestures are patterns of rising and falling intervals, and the nature of these intervals which, in certain styles, are more important than the actual intervals themselves. So, it could be that the three figures given in ex 2:1

are 'related', at least in one sense of the word, and especially when combined with related timbres, etc.
To begin with, I wrote short programmes to create a number of these 'contours'. A typical example of this might comprise, for instance, fourteen elements: A,B,C...M. A rough contour, (e.g. a composed, (usually 'chorale-type' and quite often with serial 'elements'), might be initially described, (ex 2:2)
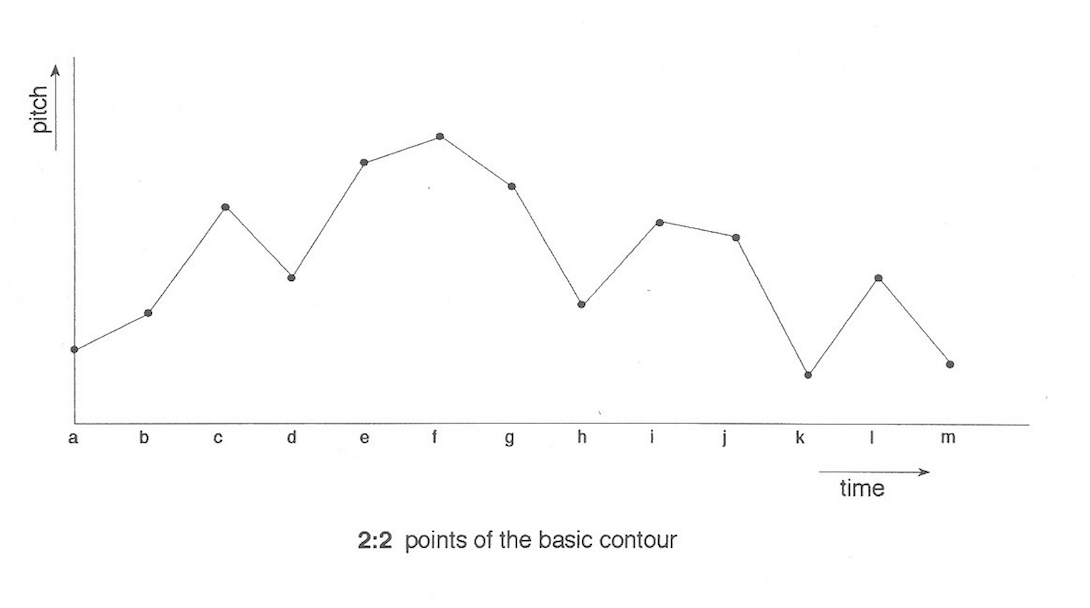
An easy way to describe this in computer terms (i.e. numerically) is to say that (< = 'is less than'; > = 'is greater than'):
A < B < C > D < E < F > G > H < I > J > K < L > M
I initially programmed the computer to look through an array of randomly generated numbers (0-1000) and come up with values that would represent this 'row'. A problem occurred almost immediately. If, for instance, the first value was 990, the next two values could often not be found, (there were no numbers higher than 990 in the array). Alternatively, the programme could produce similar anomalies at any point in the row. The results of this process generally proved to be either incomplete, or highly eccentric. Since I wanted stylistically similar results this was obviously not good.
Gradually it became necessary to be more and more specific about each point:
A > range
x }initial inputs, (i.e., makes sure the initial note is neither too high nor too low)
A < range
y
B > A
B < (A+A/2) }B is greater than A, but less than 1.5*A
C > A }C is greater than A; the gap between C and B is greater than that between B
(C-B) > (B-A) }and A, but C is not more than 0.75 of the original 'highest point' available
C < (range * 0.75) }according to the 'range' value above.
D < C
(C-D) > ((C-B/2)
D > A }and so on...
E > C
(E-C) > (C-D)
F > E
(F-E) > (E-D)
G < F
(F-G) > (C-G)
H < G
(G-H) > ((C-B) +/- ((G-H)/60)))
I > H
(I-H) > (G-H)
J < I
(I-J) < ((J-H)/3))
K < J
(J-K) > (I-H)
K > (J/4)
L > K
(L-K) < ((J-K)/2)
L < F
L-K
M < L
M < K
(L-M) < ((L-K)*2)
This is as far as the process went. Each point has an initial 'contour-reference' relating to the previous point, then a set of criteria for each value. With this programme I was able to achieve virtually any number of equivalent and yet different 'melodic streams', (I wrote another small programme for converting the numeric values into frequencies and then 'pitches'). Ironically, although some of this material was used, it is no longer recognizable as such because of further 'intuitive' editing. Although this calls into question the immediate value of the above programme it has value in as much as it makes an understanding of the varieties of randomness much more clear.
2.1.2 Rotation
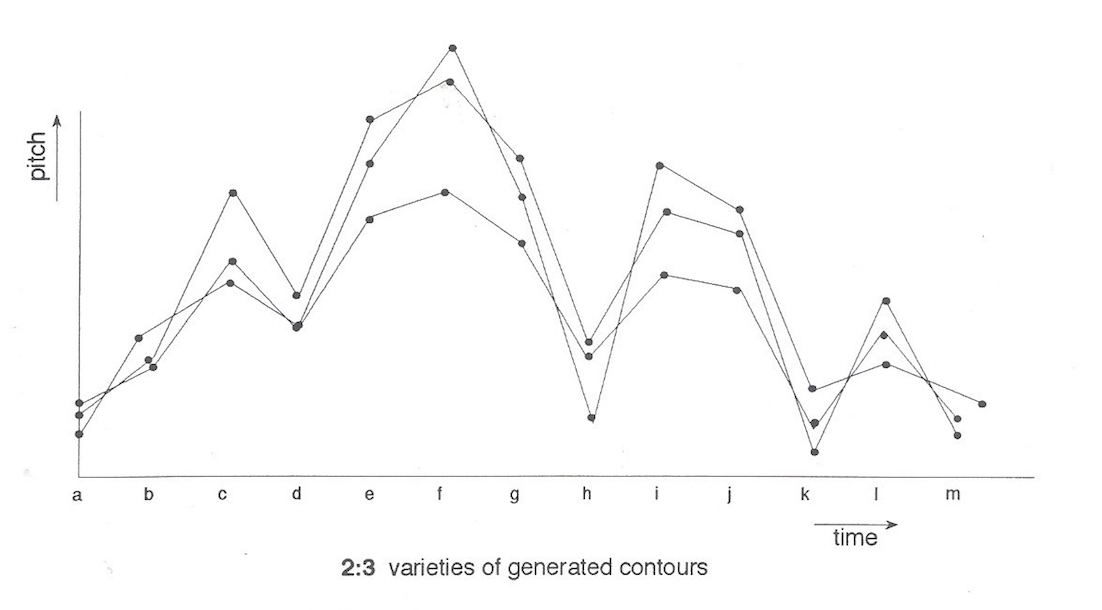
The above work with contours, when seen from the point of view of 'statistical results' had quite clear geometrical ramifications, (ex 2:3).
It occurred to me that further material of a more directed nature could be achieved by rotating these figures about a point, (ex 2:4).
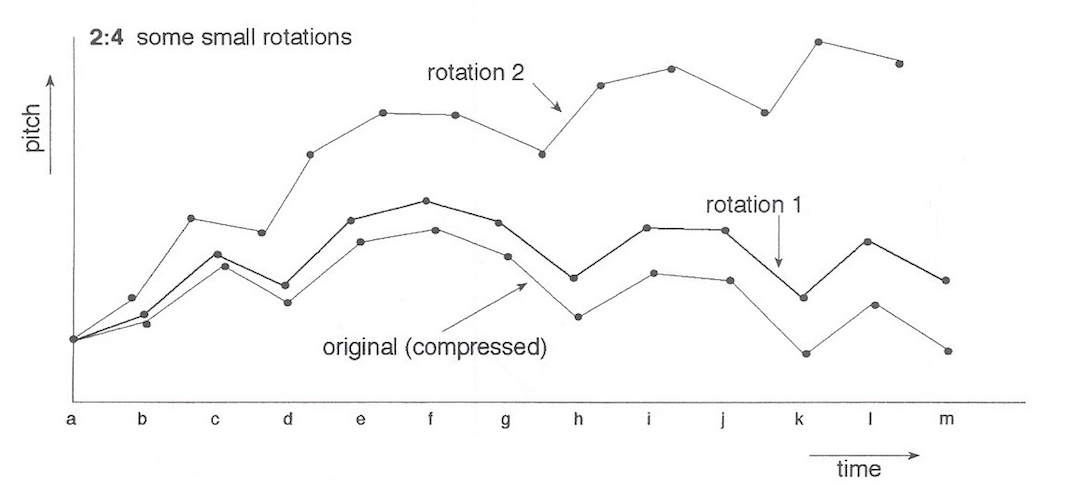
This not only produced changes in contour, while maintaining certain characteristics, but also could give 'static' line a direction. By rotating a large amount, such as (+ or -) 90 degrees, because of the movement across the (x,y) axes, a new contour could be achieved, (ex 2:5).
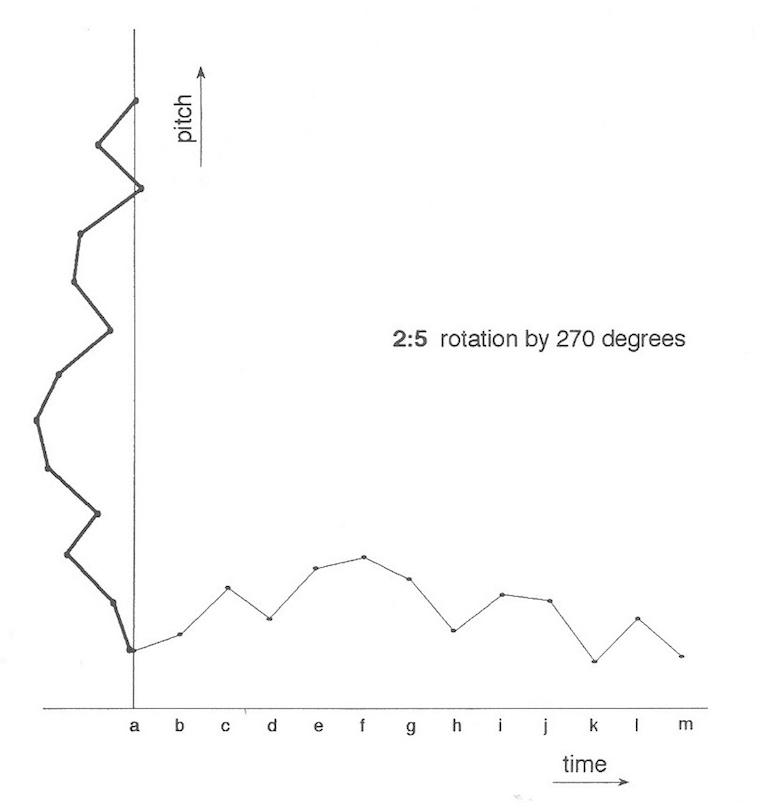
The actual result was quite complex: a long, undulating line would be translated into a short, very angular one. If this new contour were then 'time dilated', the new contour would be created (ex 2:6-2:9).
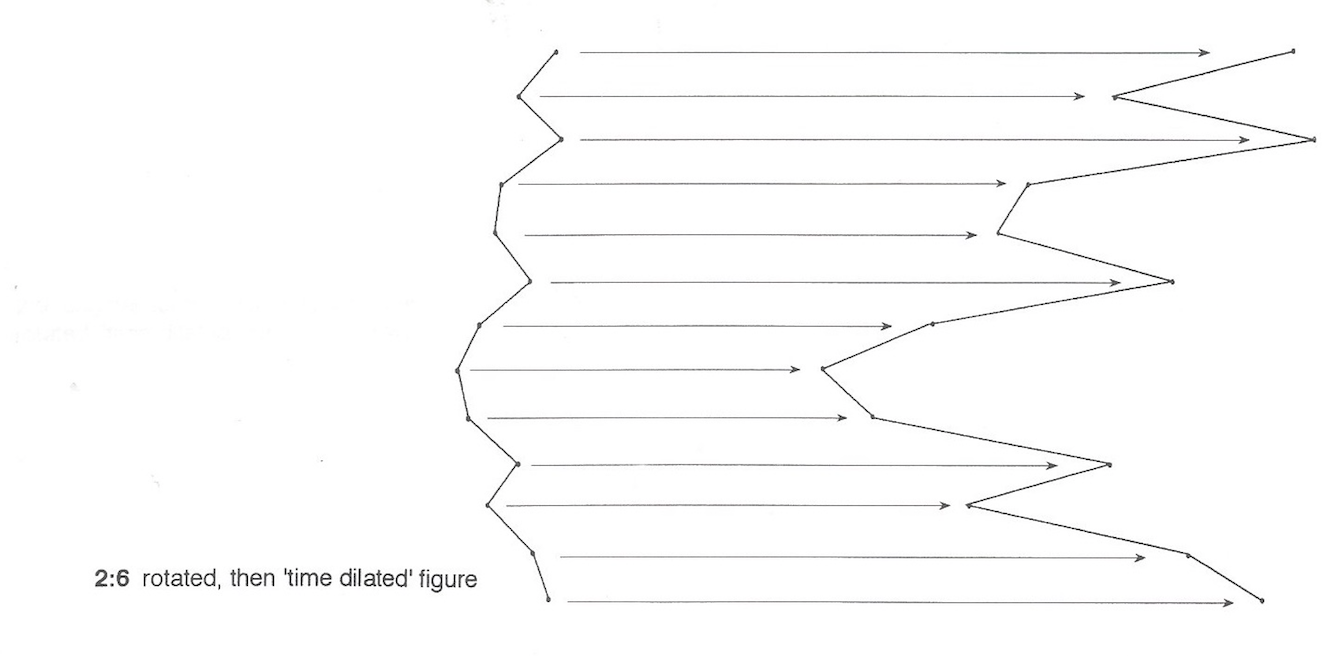
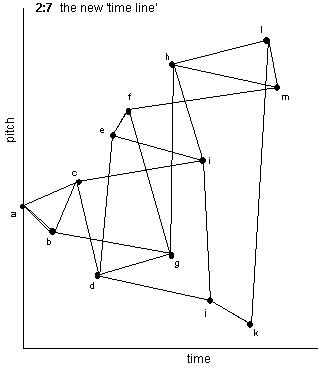

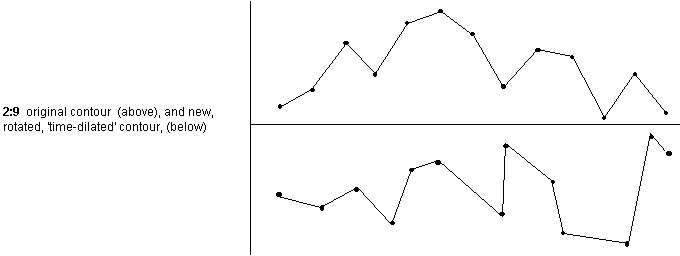
However, the 'time dilation', although interesting, seemed to remove any direct link between the original and rotated figures, so I decided to try the process using a smaller, more comprehensible figure. In ex 2:10-2:13

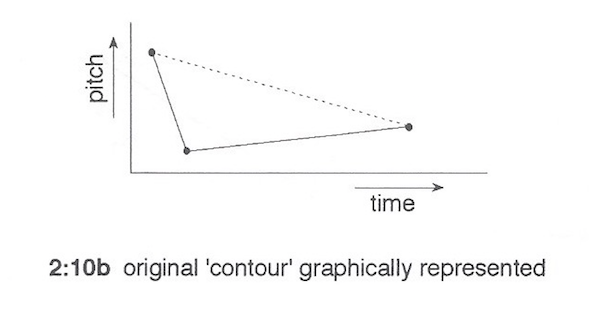
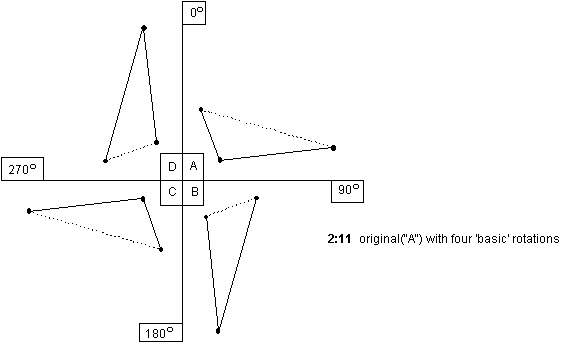
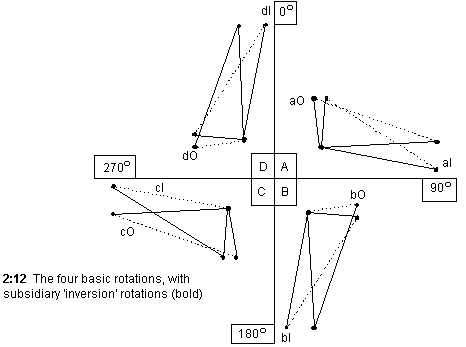
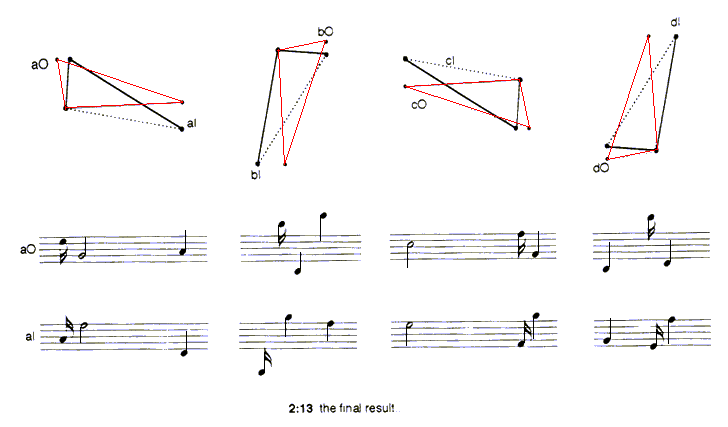
this process is illustrated using a simple three note figure that was to be the basis of the first phrase of the 'chorale' of the Sextet.
2.2 Commentary
All the above elements were utilized in the composition of the Sextet. However, there is little direct evidence, as all the processes have gone through a number of stages of intuitive editing.
Pitches were commonly generated using some sort of row, duplicating it, transposing and inverting it, possibly, and then creating a new row by taking a note from each of the derived rows alternately. The process would then be repeated. The lengthy result would then act as a basic supply of pitches, although they were never used with any particular severity or discipline, and the rows would usually be edited according to circumstance. This emphasises the nature of the role of the 'rows', however generated, in my music. They are a means to an end, a way of generating material that can be used as necessary, and, if used, altered at any point to suit other needs. They are not rows in the strictly serial sense, (although they could be used as such if necessary).
There are two main sources of material used in the piece. The first is a row based on the open strings of all the instruments in the Sextet. Ex 2:14

shows these open strings, and the row is formed by the number of semitones between each string. This produces the following row:
7 5 2 5 2 5 7 7
Matrices may be formed in a number of ways from this:
7 5 2 5 2 5 7 7
6 4 1 4 1 4 6 6
5 3 7 3 7 3 5 5
4 2 6 2 6 2 4 4
3 1 5 1 5 1 3 3
2 7 4 7 4 7 2 2
1 6 3 6 3 6 1 1
7 5 2 5 2 5 7 7
or
7 5 2 5 2 5 7 7
6 6 1 4 3 4 1 6
5 7 7 3 4 3 2 5
4 1 6 2 5 2 3 4
3 2 5 1 6 1 4 3
1 4 3 6 1 6 6 1
7 5 2 5 2 5 7 7
Matrices such as these provide much basic material for harmony and, more especially, rhythm.
The second main material used is a contour, much as those discussed above. In fact, because of the difficulties involved in manipulating large contours, in the Sextet, six smaller contours are used, which, when combined, form the phrases of a 'chorale'. Ex 2:15

shows these contours, labelled A to F. These contours provide extremely flexible, and yet (potentially) aurally clear melodic formulae. These contours, almost by default, permeate the whole piece, often not so perceivable as such, but because of the divided phrases. Although not exact, the opening phrases of the 'cellos display hints of these contours.
The contours of the opening pages build up to a more specific example of this: the violin solo, (figure J). Here, the first violinist must choose between a variety of 'routes' through the phrases, (six phrases, but D & E are elided). Each phrase is one of the contours in an interpretation of one of the four 'primary' rotations: 0, 90, 180, and 270 degrees. The 'vertical' order in which they appear is altered, to aid variation. As can be seen from ex 2:16,

the contours are interpreted with a variety of alterations and additions often to the point where they are no longer recognizable. As usual, the contours provide the basis on which the composition is based.
An example in which this method is combined with a (multiple) use of the row comes with the passage at figure T. Here, sustained chords are contrasted with fast, erratic figures. Although distorted by an accelerando, the lengths of the sustained chords outline the row, with bars of 7, 7, 5, 2, 5, 2, 5 and 7 crotchets. Similarly, the erratic interludes are 5, 6, 4, 5, 7, 5 and (originally, though finally extended), 7 quavers: a transformation of the original. In addition, the harmonies of the sustained chords are based on transformations of fifth chords, although these are very hidden, and based around the sequence of open strings descending. So, the 'primary' note of the first chord is E, the second, A, the third, D, and so on. Finally, during the erratic episodes, each instrument outlines a version of the respective contour.
Once again, the methods used here were used to enhance the basic musical idea, rather than dictating it. This passage is the culmination of a vigorous and complex contrapuntal passage, as well as marking a return to the more sustained texture of the opening. The basic idea is primary, not the method.
As usual in pieces of mine with a one movement form, the Sextet is in a very general ABA + coda form. The first A section, which ends with the latter passage, acts as a combination of exposition and organically growing introduction. The B section usually represents a more formally obvious development, often based on or starting from a very different perspective. In the Sextet, which was originally intended to be quite a short piece, this central section was to be a sort of 'cloud' of different materials, connected with what has been heard before. In order to structure the 'internal clouds', a scheme was devised based on six versions each of three different 'clouds', and six more versions of these clouds, each smaller. The smaller versions were used to connect the larger, to give a sense of perspective and movement to the otherwise rather diffuse texture. The final scheme was as follows:
A1 B1 a2 C1 B2 a6 b6 c6 C2 A2 b5 C3 a5 A3 c5 B3 a4 B4 c4 b4 A4 b3 C4 A5 C5 a3 c3 B5 a1
c2 C6 B6 c1 A6 b2 b1 [a]
A represents a series of sharp, spiccato and highly rhythmic repeated notes, (based on harmonies derived from the row). B is one or more high, harmonic, unsynchronised attacks. C is a very high semi-pitched collection of varied spiccato fragments. Lower case letters represent less substantial renderings, often forming links between the larger sections. As usual, the scheme deferred to the 'real' composition should problems have arisen.
The final A section of the overall piece usually represents a sort of truncated recap, in which the most important elements of the 'exposition' are re-interpreted in condensed form, often making much more explicit the 'central' ideas. This occurs here. At figure HH the 'recapitulation' starts, emerging from the 'clouds'. There follows brief recapitulations of the opening, (now explicitly based on each instrument's open strings), the solo melody, (now on a viola), and the 'dance' episode, originally fast and frenetic, now slow and sedate. After a brief transition (figure RR) there is a coda based on the 'cloud' material and parts of the 'chorale' combined.
Each passage of the above is constructed in a similar way to the first episodes described. The initial musical idea is planned and then methods are used to complete the detail.
2.3 MIDI Sequence & Graphic Score
As was mentioned in the Introduction, the recording of the MIDI sequence file included is not intended to represent an imitation of the actual sound, merely a guide to some of the basic textures and overall structures. Strings tones, because of their constantly varying structures are difficult both to synthesize and to manipulate via MIDI. In addition, the use of quarter-tones makes a MIDI rendition virtually impossible, as each quarter-tone has to be created using a 'standard' tuned note as a base, and this has to be altered using a separate MIDI control. I have had some doubts as to whether to include this tape or not, but have decided that, bearing all these problems in mind, it has value as a general guide to the composition.
2.4 Influences
Most of the influences on the Sextet were quite usual for me: Ligeti, (the opening to figure C is influenced by his String Quartet No 2), and Birtwistle, (the routes and mobiles), as well as the sustained passage at figure T, which now appears to be a fairly obvious imitation of a passage in The Triumph of Time. There are also passages that are reminiscent of electro-acoustic music: elements of Kontakte and The Mask of Orpheus, (the 'interruptions' that occur throughout the latter). Figure A and the rhythmic 'cloud' at figure V.